Introduction
Welcome to an in-depth exploration of the KerML and SysML v2 metamodels. Join us as we delve into the complexities of class relationships and constraints. We will examine the role of OML and its Description Logic (DL) reasoning in shedding light on the challenge presented by class LiteralBoolean, despite its apparent simplicity.
The Class Hierarchy
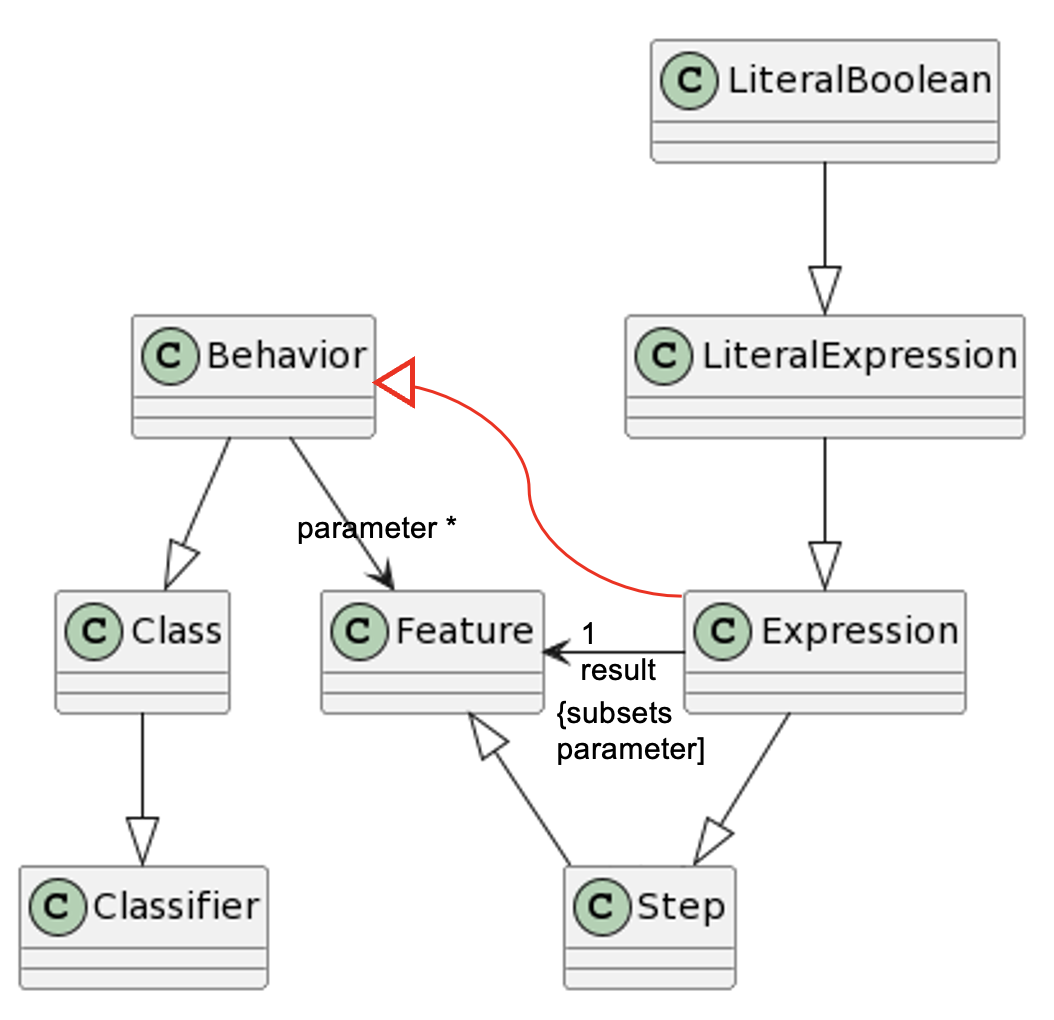
Our discussion revolves around various metaclasses: LiteralBoolean, LiteralExpression, Expression, Step, Feature, Behavior, Class, and Classifier. Each of these metaclasses plays a significant role in our analysis. LiteralBoolean is a subclass of LiteralExpression, which, in turn, is connected to Expression. This chain continues with Expression leading to Step and finally culminating with Feature. On the other hand, metaclass Behavior is a subclass of Class and, by extension, Classifier.
The Disjointness Dilemma
The class hierarchy above induces an interesting challenge. The absence of a common subclass between metaclasses Classifier and Expression leads to an inference that they are “disjoint” (through a special algorithm in OML known as the bundle closure algorithm). Moreover, the result property connects metaclasses Expression and Feature with a strict cardinality of exactly 1. This means each instance of Expression must have a result property value. Since the result property is a subproperty of the parameter property, this also means that each Expression must have a value for the parameter property. Since the parameter property has metaclass Behavior as its domain, the reasoner concludes that metalass Expression must also be a subclass of Behavior, as indicated by the red inheritance arrow in the class diagram above. However, this new inference conflicts with the earlier one that metaclasses Expression and Behavior are disjoint. This makes the two metalclass unsatisfiable (have no valid individuals). Since LiteralBoolean is a subclass of Expression, it also becomes unsatisfiable.
Conclusion
In this thorough examination of interconnected classes and underlying conflicts, DL reasoning emerges as a crucial tool for gaining a deeper understanding. As you navigate the world of metamodels and systems, it is essential to appreciate the role of DL reasoning. It transforms the concept of unsatisfiability into an exploration of the intricate web of class relationships. As you venture into the realm of KerML and SysML v2 metamodels, remember that DL reasoning serves as a guiding map, helping you navigate the complex and paradoxical terrain.